Achando a Raiz de Equações usando o Método de Newton (em F#)

Este post é uma releitura de um que havia escrito, em 2016, e que se perdeu no “reboot” do blog. Minha maior motivação para estar republicando esse post foi esse comentário.

Representando Equações

Abaixo, compartilho uma estrutura de dados simples para representar equações matemáticas em F#:

type Expr =
  | X
  | Const of value: double
  | Add   of Expr * Expr
  | Sub   of Expr * Expr
  | Mult  of Expr * Expr
  | Div   of Expr * Expr
  | Pow   of Expr * Expr
  | Neg   of Expr

// 2 + 2 / 2
let sample = Add(Const(2.), Div(Const(2.), Const(2.))

Estamos criando vários tipos em poucas linhas.

Simplificando Equações

Algumas equações matemáticas podem ser simplificadas facilmente. A implementação que segue realiza simplificações comuns em equações descritas como os tipos que acabamos de criar.

let rec simplify e =
  let result =
      match e with
      // add
      | Add(Const(0.), r) -> simplify r
      | Add(l, Const(0.)) -> simplify l
      | Add(Const(l), Const(r)) -> Const (l + r)
      | Add(l, r) -> (Add(simplify l, simplify r))
      // sub
      | Sub(Const(0.), r) -> Neg (simplify r)
      | Sub(l, Const(0.)) -> l
      | Sub(Const(l), Const(r)) -> Const (l - r)
      | Sub(X, r) -> Sub (X, simplify r)
      | Sub(l, X) -> Sub (simplify l, X)
      | Sub(l, r) -> (Sub(simplify l, simplify r))
      // mult
      | Mult(Const(0.), _) -> Const(0.)
      | Mult(_, Const(0.)) -> Const(0.)
      | Mult(Const(1.), r) -> r
      | Mult(l, Const(1.)) -> l
      | Mult(Const(l), Const(r)) -> Const (l * r)
      | Mult(l, r) when l = r -> (Pow (simplify l, Const(2.)))
      | Mult(Pow(b, p), r) when b = r -> Pow (simplify b, (simplify (Add((simplify p), Const(1.)))))
      | Mult(X, r) -> Mult (X, simplify r)
      | Mult(l, X) -> Mult (simplify l, X)
      | Mult(l, r) -> (Mult(simplify l, simplify r))
      // div
      | Div(Const(0.), _) -> Const(0.)
      | Div(l, Const(1.)) -> l
      | Div(Const(l), Const(r)) -> Const (l / r)
      | Div(X, r) -> Div (X, simplify r)
      | Div(l, X) -> Div (simplify l, X)
      | Div(l, r) -> simplify (Div(simplify l, simplify r))
      // pow
      | Pow(_, Const(0.)) -> Const(1.)
      | Pow(b, Const(1.)) -> simplify b
      | Pow(Const(l), Const(r)) -> Const(System.Math.Pow(l, r))
      | Pow(X, r) -> Pow (X, simplify r)
      | Pow(l, X) -> Pow (simplify l, X)
      | Pow(b, p) -> (Pow(simplify b, simplify p))
      // neg
      | Neg(Const(k)) -> Const (-k)
      | Neg(X) -> Neg(X)
      | Neg(x) -> (Neg(simplify x))
      //
      | other -> other
   
  if (result = e)
      then result
      else simplify result
 
simplify (Mult(Mult(X, X), X))
simplify (Pow(Const(2.), Const(3.)))
simplify (Mult(Const(2.), X))
simplify (Add(Const(2.), Div(Const(2.), Const(2.) )))

Perceba que fiz uso de uma função local (também suportado em C#).

Um efeito interessante, é que em todas as equações onde não foi utilizada uma variável, a simplificação resolve a equação.

Resolvendo equações sem variáveis

Já sabemos que a função de simplificação resolve equações desde que não tenha sido utilizada nenhuma variável. Logo, a “execução” de uma equação pode ser aplicada pela substituição da variável por um valor constante e posterior simplificação.

let exec x expr = 
    let rec replaceX = function 
        | Add(l, r)  -> Add(replaceX l, replaceX r)
        | Sub(l, r)  -> Sub(replaceX l, replaceX r)
        | Mult(l, r) -> Mult(replaceX l, replaceX r)
        | Div(l, r)  -> Div(replaceX l, replaceX r)
        | Pow(l, r)  -> Pow(replaceX l, replaceX r)
        | Neg(e)     -> Neg(replaceX e)
        | Const(v)   -> Const(v)
        | X          -> Const(x)
    
    match simplify (replaceX expr) with 
    | Const(result) -> result
    | _ -> failwith "impossible to execute"
        
// resulta 8
Pow(Const(2.), X) |> exec 3.

Interpretando strings

Quero permitir que a entrada de equações ocorra através de uma string. Para isso, “requentei” um código de um post anterior (perdido) que utiliza Active Patterns.

open System
 
let (|Digit|_|) = function
    | x::xs when Char.IsDigit(x) ->
        Some(Char.GetNumericValue(x), xs)
    | _ -> None

let (|IntegerPart|_|) input =
    match input with
    | Digit(h, t) ->
        let rec loop acc = function
            | Digit(x, xs) -> loop ((acc * 10.) + x) xs
            | xs -> Some(acc, xs)
        loop 0. input
    | _ -> None
 
"10" |> List.ofSeq |> (|IntegerPart|_|)

let (|FractionalPart|_|) = function
    | '.'::t->
        let rec loop acc d = function
            | Digit(x, xs) -> loop ((acc * 10.) + x) (d * 10.) xs
            | xs -> (acc/d, xs)
        Some(loop 0. 1. t)
    | _ -> None
 
"10" |> List.ofSeq |> (|FractionalPart|_|)
".34" |> List.ofSeq |> (|FractionalPart|_|)

let (|Number|_|) = function
    | IntegerPart(i, FractionalPart(f, t)) -> Some(i+f, t)
    | IntegerPart(i, t) -> Some(i, t)
    | FractionalPart(f, t) -> Some(f, t)
    | _ -> None
 
"10" |> List.ofSeq |> (|Number|_|)
".35" |> List.ofSeq |> (|Number|_|)
"10.35" |> List.ofSeq |> (|Number|_|)


let parse (expression) =
    let rec (|Expre|_|) = function
        | Multi(e, t) ->
            let rec loop l = function
                | '+'::Multi(r, t) -> loop (Add(l, r)) t
                | '-'::Multi(r, t) -> loop (Sub(l, r)) t
                | [] -> Some(l, [])
                | _ -> None
            loop e t
        | _ -> None
    and (|Multi|_|) = function
        | Atom(l, '*'::Powi(r, t)) -> Some(Mult(l, r), t)
        | Atom(l, '/'::Powi(r, t)) -> Some(Div(l, r), t)
        | Powi(e, t) -> Some(e, t)
        | _ -> None
    and (|Powi|_|) = function
        | '+'::Atom(e, t) -> Some(e, t)
        | '-'::Atom(e, t) -> Some(Neg(e), t)
        | Atom(l, '^'::Powi(r, t)) -> Some(Pow(l, r), t)
        | Atom(e, t) -> Some(e, t)
        | _ -> None
    and (|Atom|_|) = function
        | 'x'::t -> Some(X, t)
        | Number(e, t) -> Some(Const(e), t)
        | '('::Expre(e, ')'::t) -> Some(e, t)
        | _ -> None

    let parsed = (expression |> List.ofSeq |> (|Expre|_|))

    match parsed with 
        | Some(result, _) -> result
        | None -> failwith "failed to parse expression"


parse "2+2"  // Add(Const(2.), Const(2.))
exec 0. (parse "2+2") // 4
exec 2. (parse "x^3") 
parse "x^2-3" // Sub(Pow(X, Const(2.)), Const(3.) 

Achando a derivada de uma equação

O método de aproximação de Newton utiliza derivadas, então, resolvi implementar um método simples para gerar uma equações derivadas.

let rec deriv = function 
    | X          -> Const(1.)
    | Const(_)   -> Const(0.)
    | Add(l, r)  -> Add(deriv l, deriv r)
    | Sub(l, r)  -> Sub(deriv l, deriv r)
    | Mult(l, r) -> Add(Mult(deriv l, r), Mult(l, deriv r))
    | Neg(v)     -> Neg(deriv v)
    | Pow(b, e)  -> Mult(e, simplify (Pow(b, Sub(e, Const(1.)))))
    | _          -> failwith "expression not supported."

deriv (Pow(X, Const(3.)))

Bem-vindo, Mr Newton

Já temos todos os elementos para implementar a aproximação por Newton.

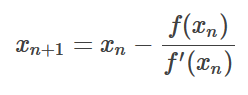
Vamos a implementação do algoritmo.

let newton expr guess error maxdepth =
    let o = parse expr
    let d = deriv o
    let eq = Sub(X, Div(o, d))

    let rec iter g depth =
        if depth > maxdepth
        then failwith "maxdepth exceeded."
        else 
            let newg = exec g eq
            printfn "%A" g
        
            if (abs (newg - g) < error)  
            then newg 
            else iter newg (depth + 1)

    iter guess 0

newton "x^3-27" 5. 0.000001 100 // 3

O método recebe uma fórmula que precisa ser resolvida, um palpite para uma solução, um erro aceitável (diferença entre duas iterações) e um número máximo de iterações permitidas.

As primeiras três linhas do método servem para “montar” a expressão. Depois, inicio a recursão verificando sempre se consegui chegar a uma aproximação boa.

Uma generalização…

let solve expr = 
    newton expr 100. 0.00001 100

solve "x^2-9"        // 3
solve "3*x^2-4*x+1"  // 1

Conclusão

Esse post é uma simples brincadeira. Fez parte dos meus esforços para aprender F#. O que achou? Gostou? Faria alguma coisa diferente? Comente