I wrote this post in 2016. Unfortunately, I lost it when I “rebooted” my blog. Anyway, I have a good friend who said this was the blog post that the most liked ever. So, I decided to bring it back (with some improvements and adjustments).
This post was originally written in Portuguese (you can see it here). I do not usually translate my posts, but I will make an exception here. Right?
In this post, I will show how to parse, simplify, differentiate and solve (using Newton’s method) equations using F#.
The Object Model
The first step to parse expressions and equations is to create a “good-enough” object model.
type Expr = | X | Const of value: double | Add of Expr * Expr | Sub of Expr * Expr | Mult of Expr * Expr | Div of Expr * Expr | Pow of Expr * Expr | Neg of Expr // 2 + 2 / 2 let sample = Add(Const(2.), Div(Const(2.), Const(2.))
It is fantastic how easy it is when using F#.
Parsing
In this implementation, I use F# Active Patterns to do the parsing.
open System
let (|Digit|_|) = function
| x::xs when Char.IsDigit(x) ->
Some(Char.GetNumericValue(x), xs)
| _ -> None
let (|IntegerPart|_|) input =
match input with
| Digit(h, t) ->
let rec loop acc = function
| Digit(x, xs) -> loop ((acc * 10.) + x) xs
| xs -> Some(acc, xs)
loop 0. input
| _ -> None
"10" |> List.ofSeq |> (|IntegerPart|_|)
let (|FractionalPart|_|) = function
| '.'::t->
let rec loop acc d = function
| Digit(x, xs) -> loop ((acc * 10.) + x) (d * 10.) xs
| xs -> (acc/d, xs)
Some(loop 0. 1. t)
| _ -> None
"10" |> List.ofSeq |> (|FractionalPart|_|)
".34" |> List.ofSeq |> (|FractionalPart|_|)
let (|Number|_|) = function
| IntegerPart(i, FractionalPart(f, t)) -> Some(i+f, t)
| IntegerPart(i, t) -> Some(i, t)
| FractionalPart(f, t) -> Some(f, t)
| _ -> None
"10" |> List.ofSeq |> (|Number|_|)
".35" |> List.ofSeq |> (|Number|_|)
"10.35" |> List.ofSeq |> (|Number|_|)
let parse (expression) =
let rec (|Expre|_|) = function
| Multi(e, t) ->
let rec loop l = function
| '+'::Multi(r, t) -> loop (Add(l, r)) t
| '-'::Multi(r, t) -> loop (Sub(l, r)) t
| [] -> Some(l, [])
| _ -> None
loop e t
| _ -> None
and (|Multi|_|) = function
| Atom(l, '*'::Powi(r, t)) -> Some(Mult(l, r), t)
| Atom(l, '/'::Powi(r, t)) -> Some(Div(l, r), t)
| Powi(e, t) -> Some(e, t)
| _ -> None
and (|Powi|_|) = function
| '+'::Atom(e, t) -> Some(e, t)
| '-'::Atom(e, t) -> Some(Neg(e), t)
| Atom(l, '^'::Powi(r, t)) -> Some(Pow(l, r), t)
| Atom(e, t) -> Some(e, t)
| _ -> None
and (|Atom|_|) = function
| 'x'::t -> Some(X, t)
| Number(e, t) -> Some(Const(e), t)
| '('::Expre(e, ')'::t) -> Some(e, t)
| _ -> None
let parsed = (expression |> List.ofSeq |> (|Expre|_|))
match parsed with
| Some(result, _) -> result
| None -> failwith "failed to parse expression"
parse "2+2" // Add(Const(2.), Const(2.))
exec 0. (parse "2+2") // 4
exec 2. (parse "x^3")
parse "x^2-3" // Sub(Pow(X, Const(2.)), Const(3.)
Simplifying and Evaluating
The following code can simplify equations/expressions removing steps to solve it.
let rec simplify e =
let result =
match e with
// add
| Add(Const(0.), r) -> simplify r
| Add(l, Const(0.)) -> simplify l
| Add(Const(l), Const(r)) -> Const (l + r)
| Add(l, r) -> (Add(simplify l, simplify r))
// sub
| Sub(Const(0.), r) -> Neg (simplify r)
| Sub(l, Const(0.)) -> l
| Sub(Const(l), Const(r)) -> Const (l - r)
| Sub(X, r) -> Sub (X, simplify r)
| Sub(l, X) -> Sub (simplify l, X)
| Sub(l, r) -> (Sub(simplify l, simplify r))
// mult
| Mult(Const(0.), _) -> Const(0.)
| Mult(_, Const(0.)) -> Const(0.)
| Mult(Const(1.), r) -> r
| Mult(l, Const(1.)) -> l
| Mult(Const(l), Const(r)) -> Const (l * r)
| Mult(l, r) when l = r -> (Pow (simplify l, Const(2.)))
| Mult(Pow(b, p), r) when b = r -> Pow (simplify b, (simplify (Add((simplify p), Const(1.)))))
| Mult(X, r) -> Mult (X, simplify r)
| Mult(l, X) -> Mult (simplify l, X)
| Mult(l, r) -> (Mult(simplify l, simplify r))
// div
| Div(Const(0.), _) -> Const(0.)
| Div(l, Const(1.)) -> l
| Div(Const(l), Const(r)) -> Const (l / r)
| Div(X, r) -> Div (X, simplify r)
| Div(l, X) -> Div (simplify l, X)
| Div(l, r) -> simplify (Div(simplify l, simplify r))
// pow
| Pow(_, Const(0.)) -> Const(1.)
| Pow(b, Const(1.)) -> simplify b
| Pow(Const(l), Const(r)) -> Const(System.Math.Pow(l, r))
| Pow(X, r) -> Pow (X, simplify r)
| Pow(l, X) -> Pow (simplify l, X)
| Pow(b, p) -> (Pow(simplify b, simplify p))
// neg
| Neg(Const(k)) -> Const (-k)
| Neg(X) -> Neg(X)
| Neg(x) -> (Neg(simplify x))
//
| other -> other
if (result = e)
then result
else simplify result
simplify (Mult(Mult(X, X), X))
simplify (Pow(Const(2.), Const(3.)))
simplify (Mult(Const(2.), X))
simplify (Add(Const(2.), Div(Const(2.), Const(2.) )))
I love local functions! The simplification process works as an evaluator for expressions. With equations, the process will stop when there are no more possible simplification steps to take.
let exec x expr =
let rec replaceX = function
| Add(l, r) -> Add(replaceX l, replaceX r)
| Sub(l, r) -> Sub(replaceX l, replaceX r)
| Mult(l, r) -> Mult(replaceX l, replaceX r)
| Div(l, r) -> Div(replaceX l, replaceX r)
| Pow(l, r) -> Pow(replaceX l, replaceX r)
| Neg(e) -> Neg(replaceX e)
| Const(v) -> Const(v)
| X -> Const(x)
match simplify (replaceX expr) with
| Const(result) -> result
| _ -> failwith "impossible to execute"
// resulta 8
Pow(Const(2.), X) |> exec 3.
Differentiating
Newton’s method will need derivatives to work. So, let’s produce it.
let rec deriv = function
| X -> Const(1.)
| Const(_) -> Const(0.)
| Add(l, r) -> Add(deriv l, deriv r)
| Sub(l, r) -> Sub(deriv l, deriv r)
| Mult(l, r) -> Add(Mult(deriv l, r), Mult(l, deriv r))
| Neg(v) -> Neg(deriv v)
| Pow(b, e) -> Mult(e, simplify (Pow(b, Sub(e, Const(1.)))))
| _ -> failwith "expression not supported."
deriv (Pow(X, Const(3.)))
Welcome, Mr. Newton
We now already have all the elements we need to solve equations using Newton’s method.
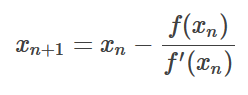
Here is my implementation.
let newton expr guess error maxdepth =
let o = parse expr
let d = deriv o
let eq = Sub(X, Div(o, d))
let rec iter g depth =
if depth > maxdepth
then failwith "maxdepth exceeded."
else
let newg = exec g eq
printfn "%A" g
if (abs (newg - g) < error)
then newg
else iter newg (depth + 1)
iter guess 0
newton "x^3-27" 5. 0.000001 100 // 3
The parameters are the equation we need to solve, a solution guess, an acceptable error, and iterations.
We can make it simpler to use:
let solve expr =
newton expr 100. 0.00001 100
solve "x^2-9" // 3
solve "3*x^2-4*x+1" // 1
That’s it
This post was written just for fun. I did it trying to learn F#. Do you like? Could I do something different? Please, give me your feedback.







