O Big-O é um conceito fundamental na ciência da computação que nos ajuda a entender o desempenho dos algoritmos. Em termos simples, o Big-O nos ajuda a medir a rapidez com que um algoritmo cresce à medida que o tamanho da entrada aumenta. Essa medida nos permite comparar a eficiência de diferentes algoritmos e selecionar a melhor opção para uma determinada tarefa.
Compreendendo o Big-O
O Big-O é representado por uma função matemática que descreve o crescimento do tempo de execução do algoritmo em relação ao tamanho da entrada. O Big-O nos dá uma ideia geral da eficiência do algoritmo e nos ajuda a prever o tempo de execução com base no tamanho da entrada.
Por exemplo, um algoritmo com tempo de execução O(n) cresce linearmente à medida que o tamanho da entrada aumenta. Isso significa que, se o tamanho da entrada for dobrado, o tempo de execução também será dobrado.
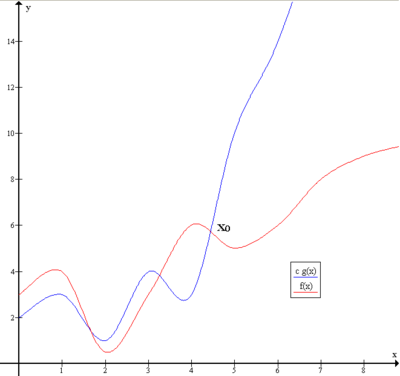
Por outro lado, um algoritmo com tempo de execução O(n²) cresce exponencialmente à medida que o tamanho da entrada aumenta. Isso significa que, se o tamanho da entrada for dobrado, o tempo de execução será quadruplicado.
Exemplos de Big-O
Veja alguns exemplos de algoritmos com seus respectivos Big-Os:
O(1): algoritmos de tempo constante, como acessar um elemento em um array ou fazer uma operação matemática simples:
public static T AccessFirstElement<T>(T[] array)
{
return array[0];
}
// Fonte: Chat GPTpublic static <T> T accessFirstElement(T[] array) {
return array[0];
}
// Fonte: Chat GPTdef access_first_element(array):
return array[0]
# Fonte: Chat GPTO(n): algoritmos de tempo linear, como percorrer um array ou lista:
void PrintList(int[] array)
{
foreach (int item in array)
{
Console.WriteLine(item);
}
}
// Fonte: Chat GPTvoid printList(int[] array) {
for (int item : array) {
System.out.println(item);
}
}
// Fonte: Chat GPTdef print_list(array):
for item in array:
print(item)
# Fonte: Chat GPTO(n log n): algoritmos de tempo quase-linear, como mergesort e quicksort:
public static int[] MergeSort(int[] array)
{
if (array.Length <= 1)
{
return array;
}
int mid = array.Length / 2;
int[] left = array.Take(mid).ToArray();
int[] right = array.Skip(mid).ToArray();
return Merge(MergeSort(left), MergeSort(right));
}
public static int[] Merge(int[] left, int[] right)
{
int[] result = new int[left.Length + right.Length];
int i = 0, j = 0, k = 0;
while (i < left.Length && j < right.Length)
{
if (left[i] <= right[j])
{
result[k++] = left[i++];
}
else
{
result[k++] = right[j++];
}
}
while (i < left.Length)
{
result[k++] = left[i++];
}
while (j < right.Length)
{
result[k++] = right[j++];
}
return result;
}
// Fonte: Chat GPTpublic static int[] mergeSort(int[] array) {
if (array.length <= 1) {
return array;
}
int mid = array.length / 2;
int[] left = mergeSort(Arrays.copyOfRange(array, 0, mid));
int[] right = mergeSort(Arrays.copyOfRange(array, mid, array.length));
return merge(left, right);
}
public static int[] merge(int[] left, int[] right) {
int[] result = new int[left.length + right.length];
int i = 0, j = 0, k = 0;
while (i < left.length && j < right.length) {
if (left[i] <= right[j]) {
result[k++] = left[i++];
} else {
result[k++] = right[j++];
}
}
while (i < left.length) {
result[k++] = left[i++];
}
while (j < right.length) {
result[k++] = right[j++];
}
return result;
}
// Fonte: Chat GPTdef merge_sort(array):
if len(array) <= 1:
return array
mid = len(array) // 2
left = merge_sort(array[:mid])
right = merge_sort(array[mid:])
return merge(left, right)
# Fonte: Chat GPTO(n²): algoritmos de tempo quadrático, como bubble sort e selection sort:
public static int[] BubbleSort(int[] array)
{
int n = array.Length;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n - i - 1; j++)
{
if (array[j] > array[j + 1])
{
int temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
}
}
}
return array;
}
// Fonte: Chat GPTpublic static int[] bubbleSort(int[] array) {
int n = array.length;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (array[j] > array[j + 1]) {
int temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
}
}
}
return array;
}
// Fonte: Chat GPTdef bubble_sort(array):
n = len(array)
for i in range(n):
for j in range(0, n-i-1):
if array[j] > array[j+1]:
array[j], array[j+1] = array[j+1], array[j]
return array
# Fonte: Chat GPTEscolhendo o melhor algoritmo
Como você pode ver, o Big-O é um conceito poderoso que nos permite comparar e escolher algoritmos com base em sua eficiência. Ao escolher um algoritmo, é importante considerar o tamanho da entrada e como ele afetará o tempo de execução.
Por exemplo, se você tiver um grande conjunto de dados para classificar, seria mais eficiente usar o mergesort (O(n log n)) do que o bubble sort (O(n²)). No entanto, se o conjunto de dados for pequeno, a diferença de tempo de execução entre os algoritmos pode ser insignificante.
Esse conteúdo é parte do material disponibilizado para os participantes do meu grupo de estudos de Algoritmos e Estruturas de Dados. Se você se interessou pelo tema, conheça também o meu curso de Introdução à Análise de Algoritmos e Big-O.


